搜索
導航
本科課程輔導
發布時間：2024-01-26 09:46
中心極限定理依賴于抽樣分布的概念，抽樣分布是從總體中抽取大量樣本后統計量的概率分布。中心極限定理表明，如果從一個總體中抽取足夠大的樣本，即使總體不是正態分布的，樣本的均值也將呈正態分布。
中心極限定理依賴于抽樣分布的概念，它是從總體中抽取的大量樣本的統計量的概率分布。通過想象一個實驗，你可以更好地理解抽樣分布：
假設你從一個總體中隨機抽取一個樣本并計算樣本的統計量，比如均值。現在你再次隨機抽取相同大小的另一個樣本，并再次計算均值。你重復這個過程很多次，最終得到很多均值，每個樣本對應一個均值。樣本均值的分布是抽樣分布的一個例子。
中心極限定理說，只要樣本大小足夠大，均值的抽樣分布將始終呈正態分布。無論總體是正態分布、泊松分布、二項分布還是其他任何分布，均值的抽樣分布都將是正態的。
正態分布是一種對稱的鐘形分布，離分布中心越遠的觀測值越少。
幸運的是，你不需要實際反復抽樣總體來了解抽樣分布的形狀。抽樣分布的均值和標準差由總體的參數決定：
抽樣分布的均值等于總體的均值。
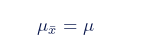
抽樣分布的標準差等于總體的標準差除以樣本大小的平方根。
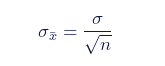
我們可以用以下公式來描述均值的抽樣分布：
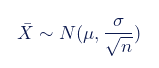
其中：
X? 是樣本均值的抽樣分布 ~ 表示“遵循分布” ，N 是正態分布， µ 是總體的均值， σ 是總體的標準差， n 是樣本大小。
樣本大小(n)是從總體中抽取的每個樣本的觀察數量。樣本大小對所有樣本都是相同的。樣本大小以兩種方式影響均值的抽樣分布。
(1)樣本大小和正態性樣本
大小越大，抽樣分布越接近正態分布。當樣本大小較小時，均值的抽樣分布有時是非正態的。這是因為只有在樣本大小足夠大時，中心極限定理才成立。
按照慣例，我們認為樣本大小為30時足夠大。
當n < 30時，中心極限定理不適用。抽樣分布將與總體的分布類似。因此，只有在總體正態時，抽樣分布才是正態的。
當n ≥ 30時，中心極限定理適用。抽樣分布將近似于正態分布。
(2)樣本大小和標準差
樣本大小影響抽樣分布的標準差。標準差是分布的變異性或擴散程度的度量(即它有多寬或多窄)。
當n較小時，標準差較大。樣本均值的擴散很大，因為它們不是總體均值的精確估計。
當n較大時，標準差較小。樣本均值的擴散很小，因為它們是總體均值的精確估計。
中心極限定理表明，在以下條件下，均值的抽樣分布將始終遵循正態分布：
樣本大小足夠大。通常，如果樣本大小為n ≥ 30，則滿足此條件。
樣本是獨立且相同分布的隨機變量。通常，如果抽樣是隨機的，則滿足此條件。
總體的分布具有有限方差。中心極限定理不適用于具有無限方差的分布，如柯西分布。大多數分布具有有限方差。
海馬課堂專業課程輔導
①3500+海外碩博導師,Highmark承諾導師真實教育背景，假一賠三!
③根據學生情況進行1V1專屬備課，輔導不滿意隨心退!
②試聽課全面升級!讓留學生聽得安心!
④課程輔導產品升級贈送考前檢驗。
⑤中英雙語詳細講解課程中的考點、難點問題，提供多方位的課后輔導!
如果你對此還有疑問,或者有更多關于學業輔導方面需求的話,可以添加微信號：hmkt131聯系海馬課堂的Joye老師哦。
